| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 플러터
- 실내 위치 예측
- 스푸핑 공격 감지 시스템
- Flutter Stack
- RSSI란?
- 실내 위치 측위
- BLE 스푸핑 공격
- Flutter Positioned
- BLE Spoofing Attack
- trilateration
- RSSI 전처리
- 삼변측량
- BLE Security
- 플러터 기초
- BLE 보안 취약
- 직선의방정식
- RSSI 평활화
- Flutter 기초
- BLE 실내 위치 측위
- 위치 정확도
- 칼만 필터
- 실내 위치 포지셔닝
- Positioned Widget
- ble
- BLE 보안
- Stack Widget
- flutter
- 해킹 감지 시스템
- BLE 삼변측량
- 삼변측량기법
- Today
- Total
컨테이너
BLE를 활용한 실내 위치 측위 (3) - 칼만 필터(Kalman Filter)를 활용한 RSSI 전처리 본문
지난 글에서 RSSI를 활용한 송신기와 수신기 사이의 거리 계산과 높은 불안정성을 보이는 RSSI의 문제점을 다뤘었습니다. 이번 글에선 칼만 필터 (Kalman Filter, K)의 간단한 정의와 칼만 필터를 사용한 RSSI의 전처리 과정을 Python 코드와 함께 알아보겠습니다.
혹시 지난 글의 내용이 궁금하신 분은 아래 링크를 참조해주세요.
BLE를 활용한 실내 위치 측위 (2) - RSSI를 활용한 거리 구하기
지난 글에선 실내 위치 측위의 필요성과 많은 무선 기술 중 왜 BLE를 사용하는지를 다뤘었습니다. 이번 글에선 어떻게 BLE를 사용하여 실내 위치 측위를 할 수 있을지 알아보겠습니다. 지난 글이
ahang.tistory.com
칼만 필터란?
칼만 필터는 지속적으로 입력되는 측정값에서 일부 알려지지 않은 변수를 고려하여 추정값을 생성하는 알고리즘입니다 [1]. 계산 과정이 단순하여 속도가 빠르고, 높은 계산 능력이 요구되지 않습니다. 따라서 칼만 필터는 노이즈가 존재하는 선형 시스템에서 신호를 처리하고 값을 예측하는 최적의 기법 중 하나로 여겨집니다 [2].
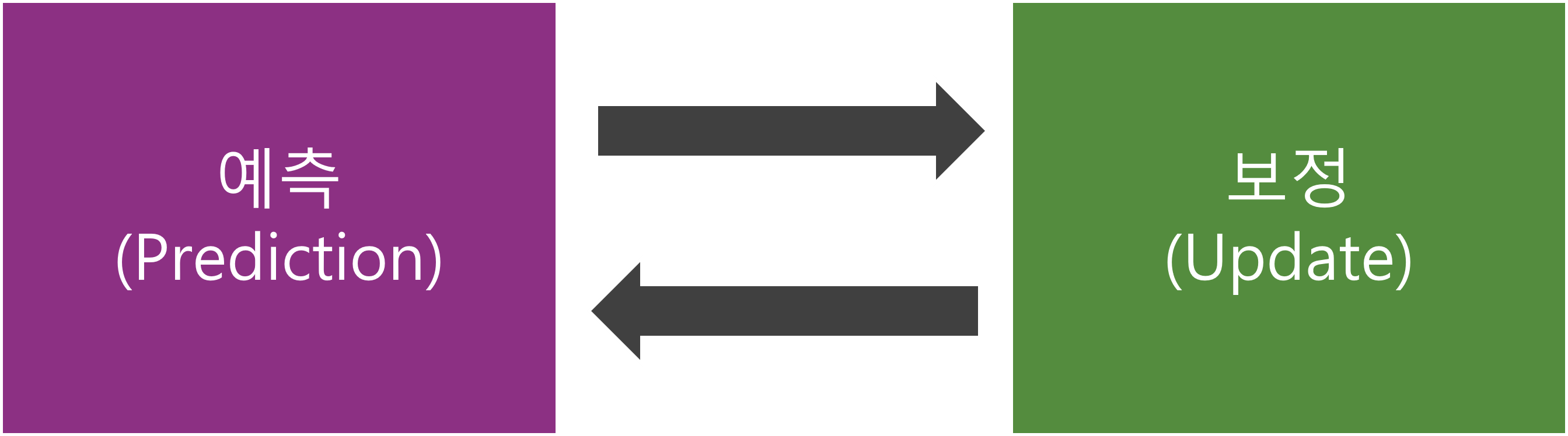
칼만 필터의 계산 과정은 위와 같이 예측과 보정 단계로 구분됩니다. 예측 단계에선 현재 측정된 RSSI를 기반으로 예측값을 추정합니다. 보정 단계에선 다음 예측값을 추정하기 위한 변수들을 현재 예측값을 기준으로 갱신합니다. 선형 시스템에선 두 계산 과정이 재귀적으로 실행됩니다.

위 그림은 선형 시스템에서의 칼만 필터 계산 과정입니다. 이전에 입력된 RSSI는 예측값을 추정에 사용되는 변수들의 값을 변화시키고, 이 변수들은 현재 측정된 RSSI를 기반으로 예측값을 생성합니다. 즉, 잡음이 포함된 이전에 수집된 RSSI를 바탕으로 다음 수집될 RSSI의 예측값을 추정합니다. 실제로 사용되는 예시를 보면 더욱 이해하기 쉬우실 겁니다.
칼만 필터를 활용한 RSSI 전처리
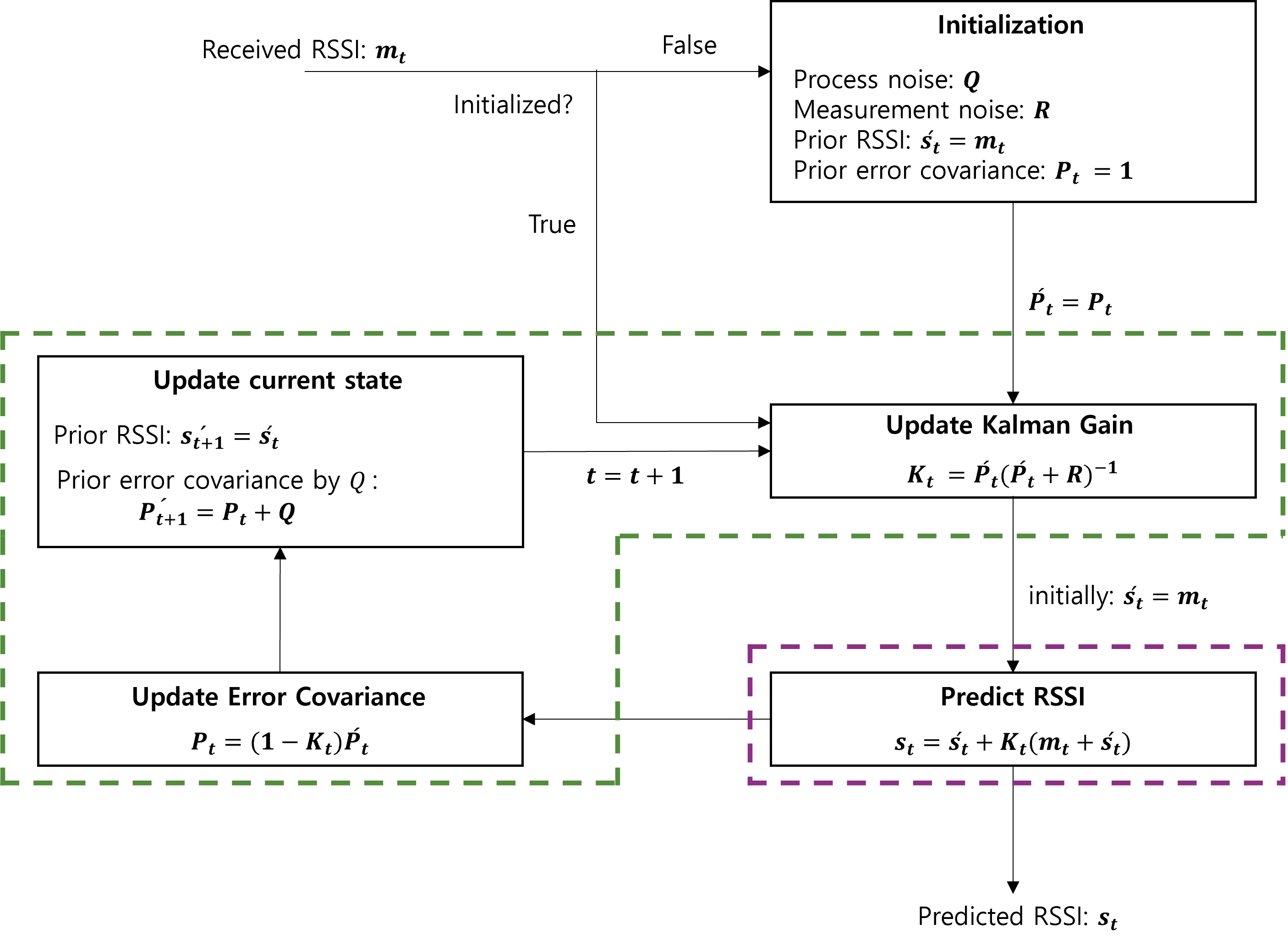
위 그림은 PFIPS [3]의 RSSI 칼만 필터링 과정입니다. 보라색 실선 부분은 예측 단계이며 초록색 실선 부분은 보정 단계를 의미합니다. 예측 단계에서 RSSI의 예측값을 추정하는 식은 아래와 같습니다.
\[s_t=\acute{s_{t}}+K_t(m_t-\acute{s_{t}})\]
$ \acute{s_{t}} $는 이전에 측정된 RSSI이고, $ m_t $는 현재 측정된 RSSI입니다. $ K_t $는 칼만 이득 (Kalman Gain)입니다. 칼만 이득은 이전에 측정된 RSSI와 현재 측정된 RSSI 중 어디에 높은 가중치를 부여할지 결정하는 변수입니다. 즉 RSSI의 예측값을 구할 때 측정된 RSSI의 노이즈가 작아 칼만 이득이 크다면 현재 측정된 RSSI에 많은 가중치를 부여하고, 오차 공분산 $ \acute{s_{t}} $가 작아 칼만 이득이 작다면 이전에 측정된 RSSI에 더 많은 가중치를 부여하여 계산합니다. 칼만 이득 $ K_t $를 구하는 식은 아래와 같습니다.
\[K_t=\acute{P_t}(\acute{P_t}+R)^{-1} \]
$ R $은 측정 노이즈 (Measurement Noise) 이며, $ \acute{s_{t}} $는 오차 공분산 (Error Covariance)으로 계산 식은 아래와 같습니다.
\[P_t=P_{t-1}+Q\]
위 식에서 $ Q $는 시스템의 노이즈입니다. 위와 같은 과정으로 RSSI의 예측값이 계산되면 보정 단계에서 오차 공분산을 새로 계산하며 보정식은 아래와 같습니다.
\[P_t=(1-K_t)\acute{P_t}\]
이렇게 업데이트 된 오차 공분산은 다음 RSSI의 예측값을 예측하는데 쓰이며, 위와 같은 단계가 재귀적으로 수행됩니다.
Python 코드
class KalmanFilter():
def __init__(self, processNoise = 0.005, measurementNoise = 20):
super(KalmanFilter, self).__init__()
self.initialized = False
self.processNoise = processNoise
self.measurementNoise = measurementNoise
self.predictedRSSI = 0
self.errorCovariance = 0
def filtering(self, rssi):
if not self.isInitialized:
self.isInitialized = True
priorRSSI = rssi
priorErrorCovariance = 1
else:
priorRSSI = self.predictedRSSI
priorErrorCovariance = self.errorCovariance + self.processNoise
kalmanGain = priorErrorCovariance / (priorErrorCovariance + self.measurementNoise)
self.predictedRSSI = priorRSSI + (kalmanGain * (rssi - priorRSSI))
self.errorCovarianceRSSI = (1 - kalmanGain) * priorErrorCovariance
return self.predictedRSSI
결과 확인
칼만 필터링 전

칼만 필터링 후
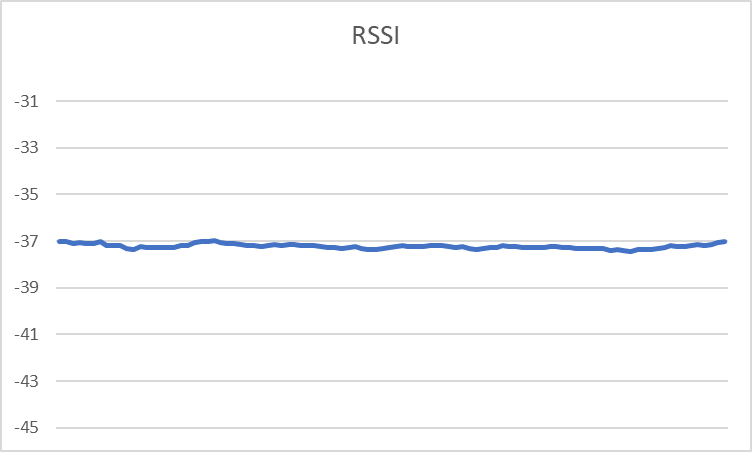
다음 글에선 칼만 필터를 통해 평활화된 RSSI를 사용한 실내 위치 측위 기법에 다룰 예정입니다.
Reference
[1] Y. Kim and H. Bang, ‘‘Introduction to Kalman filter and its applications,’’ in Introduction Implementations Kalman Filter. Rijeka, Croatia: InTechOpen, 2018.
[2] D. Simon, Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. Hoboken, NJ, USA: Wiley, 2006
[3] Y. Shen, B. Hwang, and J. P. Jeong, ‘‘Particle filtering-based indoor positioning system for beacon tag tracking,’’ IEEE Access, vol. 8, pp. 226445–226460, 2020.
'Research > Bluetooth' 카테고리의 다른 글
| BLE를 활용한 실내 위치 측위 (5) - 삼변측량 기법을 활용한 실내 위치 측위 (3) | 2022.03.02 |
|---|---|
| BLE를 활용한 실내 위치 측위 (4) - 삼변측량 기법을 사용하기 위한 예비지식 (2) | 2022.02.23 |
| BLE를 활용한 실내 위치 측위 (2) - RSSI를 활용한 거리 구하기 (0) | 2022.02.17 |
| BLE를 활용한 실내 위치 측위 (1) - 왜 BLE를 사용하는가? (0) | 2022.02.14 |
| Bluetooth Low Energy (BLE) 란? (0) | 2022.02.13 |




