| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- trilateration
- 스푸핑 공격 감지 시스템
- RSSI 평활화
- 삼변측량
- ble
- 해킹 감지 시스템
- Flutter Stack
- BLE 삼변측량
- 플러터
- Stack Widget
- Positioned Widget
- 실내 위치 예측
- 삼변측량기법
- BLE 보안 취약
- Flutter 기초
- flutter
- RSSI 전처리
- 실내 위치 포지셔닝
- BLE Security
- RSSI란?
- 직선의방정식
- 플러터 기초
- BLE 스푸핑 공격
- BLE Spoofing Attack
- 칼만 필터
- Flutter Positioned
- BLE 실내 위치 측위
- 위치 정확도
- BLE 보안
- 실내 위치 측위
- Today
- Total
컨테이너
BLE를 활용한 실내 위치 측위 (5) - 삼변측량 기법을 활용한 실내 위치 측위 본문
이번 글에선 삼변측량 기법을 활용하여 실내에서 사용자의 위치를 계산하는 방법을 알아보겠습니다. 지난 글에서 삼변측량 기법을 사용하기 위한 배경지식을 다루었었습니다. 오늘 내용을 이해하는 데 큰 도움이 되니 못 보신 분들은 아래 링크를 통해 지난 글을 먼저 보시는 것을 추천드립니다.
BLE를 활용한 실내 위치 측위 (4) - 삼변측량 기법을 사용하기 위한 예비지식
제가 작성하고 있는 BLE를 활용한 실내 위치 측위 시리즈는 삼변측량 기법을 다룰 예정입니다. 현재까지 나온 실내 위치 측위 기법 중 삼변측량 기법은 정확도가 낮은 편에 속하지만, 이 분야에
ahang.tistory.com
삼변측량 기법
아래 그림과 같은 상황에서 사용자 (Tag)의 위치를 구한다고 가정해봅시다.

사용자 (Tag)는 비콘 메시지를 송신하는 송신기의 역할을 하고, AP는 비콘 메시지를 수신하는 수신기의 역할을 합니다. 각 AP에 대해 반지름 $r_1$, $r_2$, $r_3$를 갖는 원의 방정식은 아래와 같습니다.
$$ (x-x_1)^2 + (y-y_1)^2 = r_1^2 $$
$$ (x-x_2)^2 + (y-y_2)^2 = r_2^2 $$
$$ (x-x_3)^2 + (y-y_3)^2 = r_3^2 $$
위 식의 제곱을 풀어쓴 원의 방정식은 아래와 같습니다.
$$ x^2 - 2xx_1 + x_1^2 + y^2 - 2yy_1 + y_1^2 = r_1^2 $$
$$ x^2 - 2xx_2 + x_2^2 + y^2 - 2yy_2 + y_2^2 = r_2^2 $$
$$ x^2 - 2xx_3 + x_3^2 + y^2 - 2yy_3 + y_3^2 = r_3^2 $$
이제 원의 방정식 2개를 연립하여 두 원의 교점을 지나는 방정식을 구해봅시다. AP1과 AP2의 교점을 지나는 방정식은 아래와 같습니다.
$$ 2(x_2 - x_1)x + 2(y_2 - y_1) = r_1^2 - r_2^2 - x_1^2 + x_2^2 - y_1^2 + y_2^2 $$
그리고 AP2과 AP3의 교점을 지나는 방정식은 아래와 같습니다.
$$ 2(x_3 - x_2)x + 2(y_3 - y_2) = r_2^2 - r_3^2 - x_2^2 + x_3^2 - y_2^2 + y_3^2 $$
이후의 연산에서 식이 복잡해지므로 각 항을 알파벳으로 치환하겠습니다. 치환된 항은 아래와 같습니다.
$$ A = 2(x_2 - x_1) $$
$$ B = 2(y_2 - y_1) $$
$$ C = r_{1}^{2} - r_{2}^{2} - x_{1}^{2} + x_{2}^{2} - y_{1}^{2} + y_{2}^{2} $$
$$ D = 2(x_3 - x_2) $$
$$ E = 2(y_3 - y_2) $$
$$ F = r_{2}^{2} - r_{3}^{2} - x_{2}^{2} + x_{3}^{2} - y_{2}^{2} + y_{3}^{2} $$
결과적으로 치환된 두 식은 아래와 같습니다.
$$ Ax + By = C $$
$$ Dx + Ey = F $$
우리가 구해야하는 미지수 $ x $와 $ y $는 각각 사용자 (Tag)의 x좌표, y좌표를 의미합니다. 사용자의 좌표는 위 2개의 방정식을 연립하여 얻을 수 있습니다. AP1과 AP2의 교점을 지나는 방정식을 y에 대한 식으로 이항하면 아래와 같습니다.
$$ By = C - Ax...(1) $$
\[\therefore y = \frac{C-Ax}{B}\]
위 식을 AP2와 AP3의 교점을 지나는 방정식에 대입하여 아래와 같이 $ x $를 구할 수 있습니다.
$$ Dx + E(\frac{C-Ax}{B}) = F...(1) $$
$$ (BD-EA)x = FB - EC...(2) $$
\[\therefore x = \frac{FB-EC}{BD-EA}\]
같은 방식으로 $ y $도 구해보겠습니다. AP1과 AP2의 교점을 지나는 방정식을 $ x $에 대한 식으로 이항하면 아래와 같습니다.
$$ Ax = C - By...(1) $$
\[\therefore x = \frac{C-By}{A}\]
위 식을 AP2와 AP3의 교점을 지나는 방정식에 대입하여 $ y $를 구해봅시다.
$$ D(\frac{C-Bx}{A}) + Ey = F...(1) $$
$$ (AE-DB)y = FA - DC...(2) $$
\[\therefore y = \frac{FA-DC}{AE-DB}\]
위에서 구한 사용자 (tag)의 좌표 $ x $와 $ y $를 다시 수식으로 치환하여 식을 완성합니다.
\[x = \frac{(r_2^2-r_3^2-x_2^2+x_3^2-y_2^2+y_3^2)(2(y_2 - y_1)-(2(y_3 - y_2))(r_{1}^{2} - r_{2}^{2} - x_{1}^{2} + x_{2}^{2} - y_{1}^{2} + y_{2}^{2})}{(2(y_2 - y_1))(2(x_3 - x_2))-(2(y_3 - y_2))(2(x_2 - x_1))}\]
\[y = \frac{(r_{2}^{2} - r_{3}^{2} - x_{2}^{2} + x_{3}^{2} - y_{2}^{2} + y_{3}^{2})(2(x_2 - x_1)) - (2(x_3 - x_2))(r_{1}^{2} - r_{2}^{2} - x_{1}^{2} + x_{2}^{2} - y_{1}^{2} + y_{2}^{2})}{(2(x_2 - x_1))(2(y_3 - y_2))-(2(x_3 - x_2))(2(y_2 - y_1))}\]
식은 매우 복잡한 듯 보이지만 위의 과정을 천천히 따라오셨다면 이해하는 데 큰 어려움은 없으셨을 거라 생각합니다. 이제 위 수식을 바탕으로 실내에서의 사용자 (Tag)의 위치를 측위해보겠습니다.
사용 코드
class AP:
def __init__(self, x, y, distance):
self.x = x
self.y = y
self.distance = distance
class Trilateration:
def __init__(self, AP1, AP2, AP3):
self.AP1 = AP1
self.AP2 = AP2
self.AP3 = AP3
def calcUserLocation(self):
A = 2 * (self.AP2.x - self.AP1.x)
B = 2 * (self.AP2.y - self.AP1.y)
C = self.AP1.distance**2 - self.AP2.distance**2 - self.AP1.x**2 + self.AP2.x**2 - self.AP1.y**2 + self.AP2.y**2
D = 2 * (self.AP3.x - self.AP2.x)
E = 2 * (self.AP3.y - self.AP2.y)
F = self.AP2.distance**2 - self.AP3.distance**2 - self.AP2.x**2 + self.AP3.x**2 - self.AP2.y**2 + self.AP3.y**2
user_x = ( (F * B) - (E * C) ) / ( (B * D) - (E * A))
user_y = ( (F * A) - (D * C) ) / ( (A * E) - (D * B))
return user_x, user_y
실험 가정
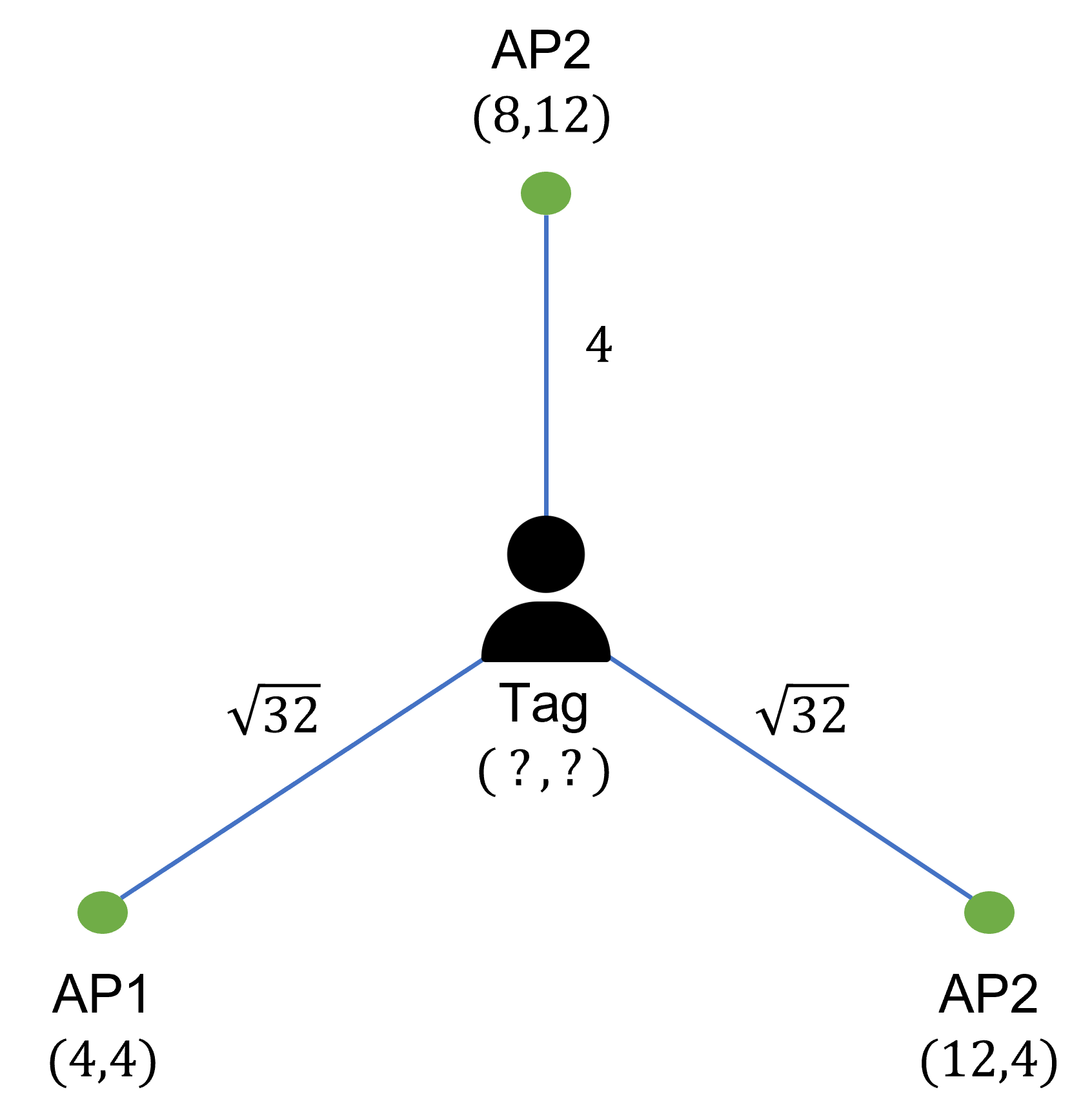
위 그림과 같이 좌푯값이 주어진 세 개의 AP를 사용하여 Tag의 위치를 계산해봅시다. AP별 Tag의 거리는 비콘 메시지의 RSSI를 활용하여 계산된 거리입니다. 따라서 실험 가정을 기반의 실행 코드는 아래와 같습니다.
if __name__ == "__main__":
ap1 = AP(4, 4, np.sqrt(32))
ap2 = AP(12, 4, np.sqrt(32))
ap3 = AP(8, 12, 4)
tril = Trilateration(ap1, ap2, ap3)
x, y = tril.calcUserLocation()
print(x)
print(y)
결과

8.0
8.0'Research > Bluetooth' 카테고리의 다른 글
| BLE를 활용한 실내 위치 측위 (4) - 삼변측량 기법을 사용하기 위한 예비지식 (2) | 2022.02.23 |
|---|---|
| BLE를 활용한 실내 위치 측위 (3) - 칼만 필터(Kalman Filter)를 활용한 RSSI 전처리 (8) | 2022.02.21 |
| BLE를 활용한 실내 위치 측위 (2) - RSSI를 활용한 거리 구하기 (0) | 2022.02.17 |
| BLE를 활용한 실내 위치 측위 (1) - 왜 BLE를 사용하는가? (0) | 2022.02.14 |
| Bluetooth Low Energy (BLE) 란? (0) | 2022.02.13 |




